Das PQ²-Diagramm der Form (Teil II)

Im vorherigen Abschnitt haben wir das p-Q²-Diagramm der Druckgussmaschine analysiert und gelernt, dass wir damit eine Vorhersage über die Bereitstellung der Schussenergie treffen können, die die Formfüllung erzeugen wird. Durch Ermitteln der p-Q²-Kurve der Form sehen wir nun, wie das Metall die von der Maschine gelieferte Energie umsetzt. Ziel ist es nun die Faktoren zu verstehen, die die Formkurve beeinflussen und welchen Einfluss wir von der Maschinenkurve bekommen.

Aus funktionaler Sicht ist die Form der Nutzer der von der Pressen-Hydraulik gelieferten Energie, die über den Kolben auf das flüssige Metall übertragen wird. Der Nutzer hat jedoch ein radikal anderes Verhalten als der Energieversorger. Während die Presse bei zunehmender Kolbengeschwindigkeit immer niedrigere Gegendrücke überwinden kann, verhält sich der Benutzer umgekehrt: Mit zunehmender Geschwindigkeit bietet die Form einen immer höheren Widerstand durch einen allmählich ansteigenden Gegendruck. In der Praxis lässt sich das sehr leicht beim Spritzen von Wasser mit einer Spritze erleben: Je mehr wir schnell und weit spritzen wollen, desto mehr müssen wir unsere Daumen auf den Kolben drücken.

 

Die Bernoulli-Formel

 

Wie ist es möglich, den richtigen Druck zu bestimmen, der auf eine Flüssigkeit ausgeübt werden muss, damit sie mit einer bestimmten Geschwindigkeit durch eine Öffnung strömt? Die Berechnung ist sehr komplex und hängt von vielen Faktoren ab und das Problem hat keine einfache Lösung. Es ist jedoch möglich, einige Vereinfachungen vorzunehmen und relativ unkomplizierte Formeln aus dem Trinkwasserinstallation zu verwenden. Im 18. Jahrhundert widmete ein Physiker namens Daniel Bernoulli einen Teil seines Lebens dem Studium des Verhaltens von Wasser in Rohren. Er beschrieb das Verhalten, indem er es in eine Formel vereinfachte, die noch heute auf den unterschiedlichsten Gebieten verwendet wird, in Wasserkraftwerken oder Springbrunnen und sogar im Druckguss.

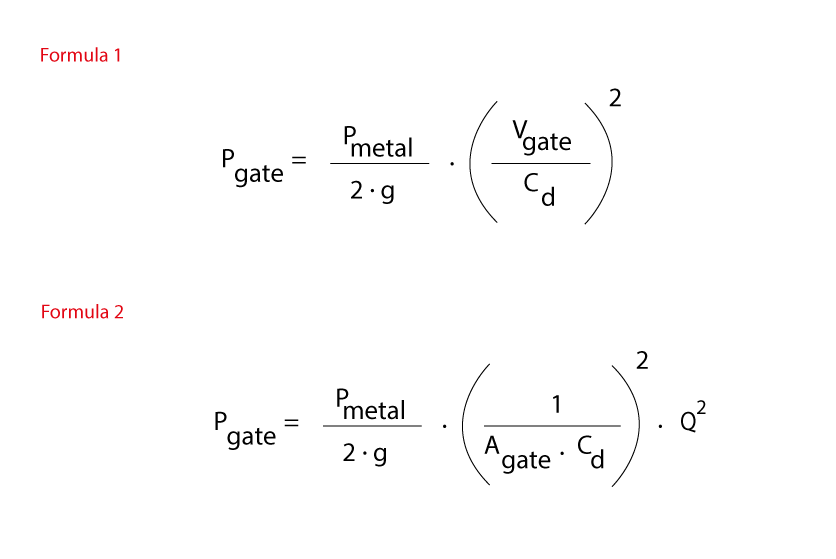
Ohne auf die mathematischen Details von Bernoullis These einzugehen, können wir vereinfacht sagen, dass der Druck, der ausgeübt werden muss, um eine Flüssigkeit (in unserem Fall die flüssige Legierung) mit einer bestimmten Geschwindigkeit durch den Anschnitt zu pressen proportional zum Quadrat der Flüssigkeitsgeschwindigkeit ist. Das heißt, um die Geschwindigkeit der Legierung zu verdoppeln, müssen wir den aufgebrachten Druck vervierfachen.

 

Formel Nr. 1

Ein anderes Beispiel haben wir beim Autofahren: mit zunehmender Geschwindigkeit steigt der Energieverbrauch überproportional an. Ab einer gewissen Grössenordnung brauchen wir für jede Erhöhung von 10% deutlich mehr als bei niedrigerer Geschwindigkeit.

Stellen wir uns eine Form mit einer bestimmten Anschnittfläche (A_gate) vor: da flüssiges Aluminium nicht komprimierbar ist, können wir sagen, dass die Durchflussmenge des Metalls (Q), das durch die Anschnittöffnungen fließt, dem Produkt der Geschwindigkeit des Metalls zum Gate multipliziert mit dem Gatequerschnitt A_gate entspricht (V_gate) . Daraus folgt, dass die Geschwindigkeit des Metalls V_gate durch das Verhältnis zwischen der Durchflussmenge Q und der Anschnittfläche A ausgedrückt werden kann. Wir können also sagen, dass die Bernoulli-Gleichung, umgeschrieben und vereinfacht für den Druckguss, besagt, dass der Druck P_gate, den der Kolben auf das Metall in der Füllkammer ausüben muss, um es mit einer bestimmten Durchflussmenge durch die Anschnittöffnungen zu drücken, proportional zum Quadrat der Durchflussmenge Q ist und umgekehrt proportional zum Quadrat des Anschnittquerschnitts A_gate.

 

Formel Nr. 2

Dies bedeutet, dass der auf das Metall ausgeübten Druck proportional zum Quadrat der Durchflussmenge ist und wir den PQ² der Maschine als gerade Linie in das PQ²-Diagramm einzeichnen können. In diesem Fall hat die Gerade jedoch eine zunehmende Steigung und schneidet sich mit der fallenden der Maschine.

Der Zusammenhang zwischen Anschnittfläche und Druck ist auch quadratisch, allerdings umgekehrt proportional: d. h. durch Vergrößern des Anschnittquerschnitts wird die Kennliniensteigung verringert, für den gleichen Volumenstrom genügt weniger Druck. Bei einer Verdoppelung des Anschnittquerschnitts ist es möglich, den Druck auf ein Viertel zu reduzieren, um die gleiche Durchflussmenge zu erhalten. Daraus folgt auch, dass die Maschine möglicherweise auch Schwierigkeiten hat, die gewünschte Füllgeschwindigkeit zu erreichen, wenn die Gießanschnitte für die Anforderungen der Form zu klein sind.

Tatsächlich hängt die Steigung der geraden Linie der Form nicht nur von der Anschnittfläche ab, sondern auch von der Dichte des betrachteten Metalls: um ein Metall mit höherer Dichte zu bewegen (zum Beispiel Zamak, das eine Dichte ρ_metal =6,2 kg/dm³) benötigen wir viel mehr Druck als für Magnesium (1,6 kg/dm³), da das Dichteverhältnis etwa 4:1 beträgt. Beladenes Auto erfordert deutlich mehr Kraft für die Beschleunigung als in leerem Zustand.

 

 

Der Widerstandskoeffizient

Ein weiterer Faktor, der in der Bernoulli-Formel berücksichtigt wird ist der Widerstandskoeffizient CD. Es ist ein Wert zwischen 0 und 1 (normalerweise im Bereich von 0,55 bis 0,7), der die “Effizienz“ des Angusssystems beschreibt und die durch Flüssigkeitsreibung verursachten Energieverluste quantifiziert, die durch eine wenig akkurate Auslegung der Gießkanäle erzeugt werden. Schlecht konstruierte Gießläufe mit abrupten Richtungsänderungen, suboptimalen Querschnitten und zu hoher Rauheit verursachen erhebliche Energieverluste, die den Metallfluss behindern.

Wieder im Automobilvergleich: Es ist intuitiv, dass das Fahren einer engen, kurvenreichen Straße mit Schlaglöchern bei hoher Geschwindigkeit ermüdender ist als das Fahren einer 4-spurigen Autobahn. Daher die Notwendigkeit, das Design der Gießkanäle, zum Beispiel mit dem CastleRUN-Modul, gründlich zu optimieren. Damit wird vermieden einen Teil der von der Maschine gelieferten Energie für Lenkungswiderstände statt Materialbeschleunigung aufzuwenden.

 

Fazit

Wir können sowohl die Kennlinie der Maschine als auch die der Form auf demselben p-Q²-Diagramm zeichnen und sehen, wo sie sich schneiden. Das heißt, der von der Maschine auf das Metall ausgeübte Druck entspricht dem Gegendruck, den der Anschnitt ausübt. An diesem Punkt ist die abgegebene Kraft gleich der Widerstandskraft, und wir haben die „Höchstgeschwindigkeit“ des Fahrzeugs identifiziert: Auch wenn wir das Gaspedal weiter betätigen, erhöht das Auto seine Geschwindigkeit nicht. Es ist so möglich, zu verstehen, ob eine Form, die auf einer bestimmten Maschine montiert ist und einen bestimmten Kolbendurchmesser verwendet, durch einen bestimmten Volumenstrom Q gefüllt wird, wenn die Anschnitte entsprechend dimensioniert sind.

Folglich besteht der nächste Schritt darin, auf dem p-Q²-Diagramm einen optimalen Arbeitsbereich für die Produktion eines bestimmten Bauteils zu identifizieren und dann alle Informationen zusammenzustellen, um zu überprüfen, ob die getroffenen Entscheidungen bei der Dimensionierung des Anschnittes, des Kolbens und der Maschine richtig sind.