Nel precedente articolo abbiamo analizzato il diagramma PQ2 dell’iniezione della pressa e capito che serve a prevedere come la macchina può erogare l’energia per riempire di metallo la cavità dello stampo. Ora, disegnando la curva PQ2 dello stampo, vedremo come il metallo utilizza l’energia messa a disposizione dalla macchina. Cercheremo anche di capire quali sono i fattori principali che influenzano la curva dello stampo e come questa interagisca con quella della pressa.
Dal punto di vista funzionale, lo stampo è l’utilizzatore dell’energia erogata dal sistema idraulico della pressa che viene trasmessa al metallo liquido attraverso il pistone di iniezione. Un utilizzatore, tuttavia, ha un comportamento radicalmente diverso da quello dell’erogatore di energia. Mentre la pressa all’aumentare della velocità del pistone riesce a vincere pressioni sempre più basse, l’utilizzatore si comporta in maniera opposta: all’aumentare della velocità, offre una resistenza sempre più elevata sotto forma di una contropressione via via crescente. Lo possiamo sperimentare facilmente cercando di spruzzare dell’acqua con una siringa: tanto più vogliamo spruzzarla velocemente e lontano, tanto più dobbiamo fare forza con il pollice sul pistone.
La formula di Bernoulli
Come è possibile determinare la pressione che è necessario esercitare su un fluido per poterlo far transitare da un foro con una determinata velocità? Il calcolo è estremamente complesso e dipende da tantissimi fattori ed il problema non è risolvibile semplicemente. È però possibile effettuare qualche semplificazione ed utilizzare delle formule relativamente semplici prese a prestito dall’idraulica. Andando indietro nel tempo fino al XVIII secolo, un fisico di nome Daniel Bernoulli dedicò parte della sua vita allo studio del comportamento delle acque nelle tubazioni e teorizzò il loro comportamento, semplificandolo, con una formula che anche oggi viene ancora utilizzata nei campi più disparati dalle centrali idroelettriche, alle fontane… alla pressocolata.
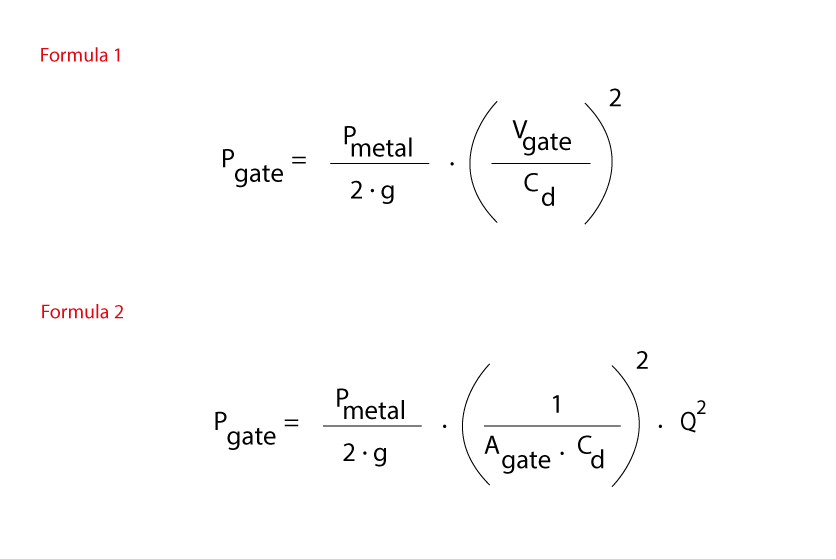
Senza entrare nel dettaglio matematico di quanto dice Bernoulli, possiamo affermare in estrema sintesi che la pressione che bisogna esercitare per far scorrere un fluido (nel nostro caso la lega liquida) attraverso una feritoia (attacco di colata) con una certa velocità (velocità agli attacchi di colata) è proporzionale al quadrato della velocità del fluido. Ovvero, per raddoppiare la velocità del fluido dobbiamo quadruplicare la pressione applicata.
Formula n° 1
Ritornando al paragone automobilistico, ci rendiamo subito conto che tutto sommato è la stessa cosa che succede alla guida di un veicolo: raddoppiare la velocità significa consumare molto di più del doppio e per raggiungere velocità elevata abbiamo bisogno di erogare una potenza molto elevata.
Se pensiamo ad uno stampo che ha una determinata area di attacco di colata Agate, posto che l’alluminio liquido non è comprimibile, possiamo affermare con certezza che la portata di metallo Q che transita dagli attacchi di colata è data da prodotto della Vgate velocità del metallo agli attacchi moltiplicato per l’area Agate degli attacchi di colata. Ne deriva che la velocità del metallo Vgate è data dal rapporto tra la portata Q e l’area dell’attacco di colata. Quindi possiamo affermare che l’equazione di Bernoulli, riscritta e semplificata per la pressocolata, afferma che la pressione Pgate che il pistone deve esercitare sul metallo nel contenitore per spingerlo con una certa portata attraverso gli attacchi di colata di sezione Agate è proporzionale al quadrato della portata Q ed inversamente proporzionale al quadrato dell’attacco di colata.
Formula n°2
Ciò significa che la correlazione tra pressione esercitata sul metallo e la sua portata è quadratica e, come per il PQ2 della macchina, posso disegnarla come una retta sul diagramma PQ2. Infatti si tratta esattamente delle stesse pressioni P e portata Q che esprime il diagramma della macchina. In questo caso, però, la retta avrà una pendenza crescente e si andrà ad intersecare con quella decrescente della macchina.
Il legame che c’è tra area di attacco di colata e pressione è quadratico ma inverso: ovvero aumentando la sezione di attacco di colata la retta dello stampo si abbassa, ovvero per raggiungere la stessa portata (o velocità) la macchina fa meno fatica perché deve esercitare una pressione inferiore. In poche parole, raddoppiando la sezione dell’attacco di colata, è possibile ridurre ad un quarto la pressione per mantenere la stessa portata. Ne deriva che se gli attacchi di colata sono troppo sottodimensionati rispetto alle esigenze dello stampo, la macchina potrebbe anche avere difficoltà a raggiungere la velocità di riempimento desiderata.
A dire il vero, la pendenza della retta dello stampo dipende, oltre che dall’area dell’attacco di colata, anche dalla densità del metallo considerato: spingere un metallo con una densità elevata (la Zama, per esempio, che ha densità rmetal =6.2 kg/dm3) richiede molta più pressione rispetto al Magnesio (1,6 Kg/dm^3) in virtù del fatto che il rapporto tra le loro densità è di circa 4:1. D’altronde intuiamo facilmente come accelerare una vettura a pieno carico richieda molta più forza che accelerare la stessa vettura vuota.
Il Coefficiente di Scarico
La densità non è l’unico fattore che interviene nella formula di Bernoulli: c’è un altro parametro detto “Coefficiente di Scarico” che altro non è che un valore compreso tra 0 ed 1 (solitamente nel range 0,55-0,7) che indica il “rendimento” del sistema idraulico ovvero quantifica forfettariamente in qualche modo le perdite di energia causate degli attriti del fluido e da un disegno poco accurato dei canali di colata. Canali di colata disegnati male, con cambi di direzione bruschi, sezioni non ottimali e rugosità troppo elevata causano perdite di energia significative che ostacolano il flusso del metallo.
Tornando al paragone automobilistico, è intuitivo che percorrere ad alta velocità una strada stretta, tortuosa e piena di buche è più faticoso che percorrere un’autostrada a 4 corsie. Da qui la necessità di effettuare una ottimizzazione spinta del disegno dei canali di colata, con il modulo CastleRUN per esempio, al fine di evitare che parte dell’energia erogata dalla macchina venga dispersa inutilmente e non venga correttamente trasferita al metallo liquido.
In Conclusione
Concludendo il discorso, possiamo tracciare sia la retta della macchina che quella dello stampo sullo stesso diagramma PQ2 e vedere dove si intersecano tra di loro: ovvero dove la pressione erogata dalla macchina sul metallo equivale alla contropressione che l’attacco di colata esercita. In questo punto la forza di spinta equivale a quella resistente ed ho individuato quindi la “velocità massima“ del veicolo: se anche premo ulteriormente l’acceleratore, la macchina non aumenta la propria velocità. Risulta quindi ovvio che da una analisi di questo tipo si possa capire se un determinato stampo, montato su una determinata macchina che utilizza un certo diametro di pistone possa lavorare spostando una portata di metallo Q (o, equivalentemente, una velocità del pistone) sufficiente a riempire correttamente lo stampo e se gli attacchi di colata siano correttamente dimensionati.
Il passaggio successivo consisterà quindi nell’individuare sul diagramma PQ2 una zona di lavoro ottimale per la produzione di un certo componente e quindi utilizzare il tutto per verificare che le scelte operate nel dimensionamento dell’attacco di colata, del pistone e della macchina siano idonee.

